Вернуться назад
Распечатать
Як вирішувати систему рівнянь у "Маткаде"? Поради та рекомендації
Математична програма MathCAD застосовується при складних алгебраїчних розрахунках в той час, коли вони утруднені або неможливі вручну. Даний ресурс значно полегшує життя багатьом технічним, економічним спеціальностями і студентам. Дуже просто змоделювати якусь задачу в математичному вигляді і отримати бажану відповідь. Однак інтерфейс може бути незрозумілий для новачків, і їм важко адекватно сприймати цю обчислювальне середовище. Одним з каменів спотикання стає те, як вирішувати систему рівнянь "Маткаде". Це дуже важлива функція, яку треба вивчити всім, хто бажає продовжувати працювати в цій програмі.
Рівняння в початковому вигляді не має коренів. Корені рівняння знаходяться на досить далекій відстані від початкового наближення. Рівняння зазнає розрив між початковим наближенням і корінням. Рівняння має максимум і мінімум між початковим наближенням і корінням. Рівняння має комплексний корінь за умови, що початкове наближення було речовим.
Щоб вирішити систему лінійних рівнянь "Маткаде", можна використовувати деякі інші варіанти. Перший спосіб полягає в тому, що ми пишемо нашу систему рівнянь через оператор if. У другому методі необхідно вдатися до методу логічних множників. Будуємо швидкий графік, натиснувши на комбінацію клавіш Shift + 2. У вікні графіка вписуємо функцію в середній вертикальний блок і в нижній вертикальний блок - аргумент "х".
Задаємо дану функцію в математичному вигляді, який зможе обробити обчислювальне середовище. Будуємо графік функції клавішами Shift + 2 позначивши функцію у вертикальному середньому віконці. У горизонтальному встановлюємо кордону, як і на інтервалі: від -10 до 10 - і вписуємо аргумент "х" у середню клітинку. Тепер нам необхідно візуально позначити нулі на графіку. Зробити це можна, додавши функцію 0 (вводиться в середню вертикальну клітинку за допомогою символу ","). Стало візуально зрозуміліше, де знаходяться нулі функції. Час провести табуляцію на графік, але при цьому потрібно задати діапазон значень. У розглянутому випадку будемо мати x:=-105 7 (двокрапка ставиться за допомогою клавіші ";". Тепер простежимо зміну знака, оцінивши значення f(x).
Як у "Маткаде" вирішити систему рівнянь
Насправді це не є простим завданням, але на розглянутих прикладах можна навчитися їх вирішувати. Дуже часто користувачі стикаються з системами рівнянь і поняттям "параметр". В математичній робочої середовищі параметр і те, як вирішувати систему рівнянь у "Маткаде", перебуває з допомогою допоміжної функції root. Крім того, що нам доведеться залучати цю функцію рішення, нам також знадобиться значення початкового наближення. Взагалі, видів систем рівнянь кілька, тому будемо розглядати конкретно на різних типах. Обговоримо, з якими проблемами може зіткнутися користувач при застосуванні функції root.Рівняння в початковому вигляді не має коренів. Корені рівняння знаходяться на досить далекій відстані від початкового наближення. Рівняння зазнає розрив між початковим наближенням і корінням. Рівняння має максимум і мінімум між початковим наближенням і корінням. Рівняння має комплексний корінь за умови, що початкове наближення було речовим.
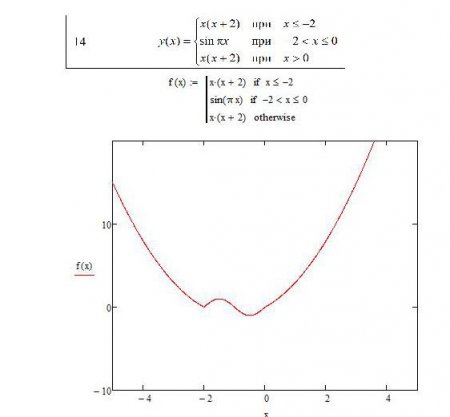
Складна функція та її графік
Почнемо з самого простого і злегка віддаленій теми, щоб поступово ввести в курс справи початківців користувачів. Це необхідно для того, щоб символьно вирішити системи рівнянь "Маткад", але спочатку спробуємо побудувати графік складної функції. Користувачеві потрібно привести формулювання в математичний вигляд, щоб графік функції побудувався коректно - так як ми маємо три ділянки, є сенс скористатися програмної конструкцією. Щоб здійснити правильну запис рівняння, скористаємося блоком if-otherwise.Щоб вирішити систему лінійних рівнянь "Маткаде", можна використовувати деякі інші варіанти. Перший спосіб полягає в тому, що ми пишемо нашу систему рівнянь через оператор if. У другому методі необхідно вдатися до методу логічних множників. Будуємо швидкий графік, натиснувши на комбінацію клавіш Shift + 2. У вікні графіка вписуємо функцію в середній вертикальний блок і в нижній вертикальний блок - аргумент "х".
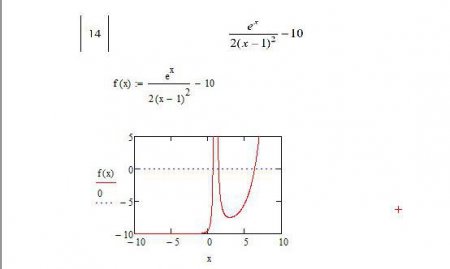
Система нелінійних рівнянь
Для нелінійних рівняння порядок знаходження коренів мало чим відрізняється від іншого типу. Припустимо, маємо функцію f(x) = (e^x/(2(x-1)^2)-10 в інтервалі від -10 до 10 включно. Перед тим, як вирішити систему нелінійних рівнянь в "Маткаде", потрібно побудувати графік, щоб оцінити нулі і скористатися вкладкою.Задаємо дану функцію в математичному вигляді, який зможе обробити обчислювальне середовище. Будуємо графік функції клавішами Shift + 2 позначивши функцію у вертикальному середньому віконці. У горизонтальному встановлюємо кордону, як і на інтервалі: від -10 до 10 - і вписуємо аргумент "х" у середню клітинку. Тепер нам необхідно візуально позначити нулі на графіку. Зробити це можна, додавши функцію 0 (вводиться в середню вертикальну клітинку за допомогою символу ","). Стало візуально зрозуміліше, де знаходяться нулі функції. Час провести табуляцію на графік, але при цьому потрібно задати діапазон значень. У розглянутому випадку будемо мати x:=-105 7 (двокрапка ставиться за допомогою клавіші ";". Тепер простежимо зміну знака, оцінивши значення f(x).